The convolution product kernel (also commonly referred to as MAC - Multiply Accumulate loop) is a basic building block for many DSP functions; it is calculated according to the following formula:

   y[n] = Sum(h[k]x[n-k]), k in [-P/2, P/2-1]

This formula calculates an element y[n] of the output vector y[], given the weights vector h[] has P values.

 

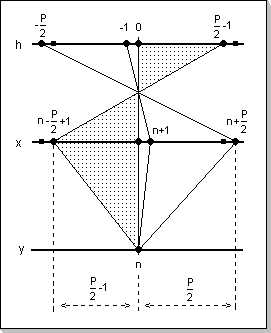
Fig.1: Calculation of an element of the convolution product output vector

The natural choice for the definition domain of vectors results to be -L to L-1, where L is in this case P/2 (note that in some cases such as the FFT and iFFT, some internal vector data manipulation will be made on a 0 to L-1 domain, but the internal use of such vectors will be transparent to the user).

The CPK formula has a number of variation that are used at the core of vector and matrix multiplication. In these cases the vectors are generally defined on the 0 to L-1 domain.

There are cases (such as the calculation of the full convolution product output vector) when the ability to address a vector outside its definition domain can be "useful" (although this could be avoided by having a larger, zero-extended, definition domain for the vectors). For these cases a new type of vector will be introduced: an Extended Vector is defined as a vector for which an attempt to read a value outside its definition domain will return Zero, while an attempt to write an element position outside the definition domain will result in no operation.